ひ~,暑い~・・・と午前中散髪に出かけて汗をかきまくった後,昼過ぎからどんより曇ってきた。明日以降は中国まで伸びた梅雨前線沿いに九州方面から東海にかけて低気圧が通過し,大雨になるとの予想。もう梅雨入り宣言しても良いのでは?
2ヶ月ぶりの散髪と,2週間ぶりの掃除洗濯を済ませて汗をかく。う~ん,ここんとこチマチマと仕事後に水泳に勤しんでいるのだが,こういう家事労働の方が結構しんどいモンである。しかしまぁ,ちゃんとしておくと気持ちが良いので,なるべく週一ペースを維持したいもの。頑張りましょう。
行きつけの町の本屋さんで,国立新美術館の案内パンフレットをもらってくる。

本屋さんと立ち話の中で,昨年見たゴーギャン展の話題になる。平日に行ったせいもあるのだろうが,あんまし混雑していなかった。しかし今回のこれはゴッホが入っているから,相当な人混みなるんじゃないかという予測を立てる。
「ゴーギャンよりゴッホの方が圧倒的に人気あるし」
「何でかね?」
「やっぱり,切られた人より切った人の方が芸術家としては偉大なんでしょう」
来週東京行きが入ったので(行かなくても良さそうだけど,どんなもんなのか見てみたいし),時間作って見てみようかなぁ。ワシのお気に入りはルソー,圧倒的にルソーなのである。
偉大にならなくてもいいので,切る方には回らないようにしたいと思いつつ,Videonews見てから寝ます。
5/19(水) 掛川・?
ひょ~,明日・・・じゃない今日締め切りの原稿,まだ影も形もないぞ,と。超特急で仕上げねばならんのだが,まだ構成を頭の中で練ってたりする。締め切りぎりぎりまで何もしないくせに焦りだけが募っていく漫画家は山ほど存在するが,今ワシは彼らの気持ちが少し理解できるようになっている。積極的にはなれない仕事だが,やらねばならん・・・となれば少しでも良いものを・・・と,現実逃避しつつ仕事に立ち向かっているという二律背反的状況,なってみると結構良いモンである。ま,何とかなるでしょ,何とかしてきたし(人ごとモード)。
夏の実験講座,今年は受講生が12名と多くなるのでPCを追加せねばならん。つーことで,近場のショップで売ってたZOTAC ZBOX HD-ND01を2台購入。光ドライブ以外はHDD 160GB, 2GB RAM,wLAN + GbE,とてんこ盛りのAtom 330 + IONマシン。Windows 7 x64 Enterpriseをインストールしようとしたらいきなりブルースクリーンの後,ビープ音が鳴りまくって起動せず。つーことで1台は初期不良ということでショップに引き取ってもらい,残り一台にインストール。これは無事済んだ・・・が,いきなり印象が悪くなったな。まぁ高々3.4万円のマシンだから,期待しちゃいかんのだろうが。

Experience Indexはこんな感じ。最初からIONドライバが入っているところはさすが最新OSだけのことはある。
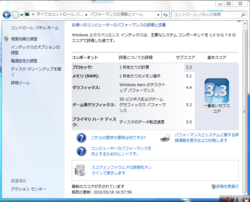
CPU以外はまぁまぁか。自宅で使っているAthlon64 X2 3800+マシンが
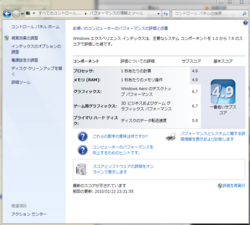
こんな感じなので(グラフィックスカードは取っ替えてある),ちょっとトロい一昔前のマシンという感じ。ま,実習用に使うだけだからいいか。
120m泳いだのでもう寝ます。
5/18(火) 掛川・?
ふ~,やっと夏も近づく八十八夜になって少し暖かくなってきた。今週は一気に気温が上がるようだが,肌寒い夜はまだ続くんだろうな。
金曜日にクラウドEXPO見学してすっかり疲れてしまった。いろんなコンピュータ関係の展示会をまとめて開催しちゃってるモンだから,コミケ並に西館から東館,全部使っているんだもんなぁ。

それでも人混みはさほどではなし。やっぱ,コミケの人混みはギネス級だ。
大まかな感想としては,デジタル化の波はあらゆる所に押し寄せてざばんと全部一度さらってしまって,今は2回目,3回目の波にジャボジャボ洗われているなという感じ。Core i7を載っけたっちっちゃいPCボードあり,秋葉原の量販店店頭には決して並ばない東芝のマザボがあったり,何のための負荷分散装置なのかよく分からないものあり(説明員に突っ込みを入れたらやっと分かったけど),見慣れたデバイスやらシステムがどんどん堅牢になり,カスタム化されているなという感じ。
大雑把にだが,全館くまなく見て回ったのでくたびれてしまい,土日はばったり。やっと復活してきたところであるが,明日・・・じゃない今日中に明日締め切りの原稿を書かねばならんのであった。懸案の原稿は一通りできたまま放置プレイ状態なので,今週中にケリをつけねばならん。来週の講演準備もあるし,キャンパスニュースの原稿も写真撮りもあるし・・・・け~,鬱病患者にはつらいスケジュールでござんす~。
GWに無許可翻訳載っけたけど,全然反響ないなw。どっかから苦情が来ればネタになるかと思ってたのに~。ま,読む人極端に少なさそうな専門書だからなぁ。唐沢俊一さんみたいに,裁判沙汰にもならないトラブルで大盛り上がりするってのはちと羨ましい。
いろいろ漫画も小説もエッセイも読んでるんだけど,全然ぷちめる暇ないな~,つーか,暇より気力の問題なんだけどさ。書き始めさえすればどーにかなるんだが,どーもそのきっかけが作れない今日この頃なのである。
そんなわけでもう寝ます。
5/11(火) 掛川・曇時々雨
何だ何だ,GWも終わったというのに,夏も近づく八十八夜だというのにこの寒さは。先月片付けてしまった,机の下に電気温風器につい手が伸びてしまったではないか。冷え冷え~。おかげで今年は風邪引きが多いようで,学生さんも初回の講義とか肝心要の時に欠席したりする。健康も学力の支えであることを痛感。
あ~,テキスト執筆,全くやる気が起きず,書き直すことだけを決意した第一章の構成を頭の中でこねくり倒すだけで一日が終わってしまった。もう金輪際,共著なんぞ書かんぞ,んっとに。つくづく嫌気がさしてきたので,明日明後日で決着をつけてやる所存。そのままぶん投げてお仕舞いにしよう。もう原稿見るのもいやじゃ。
レジストしてあったMathWorksのAcademic Virtual Conference,開幕したようなのでログインしてみる。
たくさん講演が揃えてあってまだちらっと見ただけだが,あらかじめ録音してあった著者の音声と共にスライドがめくられていく。ふ~ん,Matlab使ってPBL方式の実習をやっているのか。さすが××にあふれている(つーか,あふれてない奴は容赦なく無視する)欧米の大学は違うワイと感心。ま,□□□□□を何とか救済しようという精神ではPBLなんて出来やしませんがね。モチベーションを損なうやり方をしちゃいかんが,××がない奴のフォローばっかりしてるとPBLとは言えないものになる。難しいよなぁ。
久々に泳いできたのでもう寝ます。GW中はサボっちゃったから,落ちた筋肉を取り返さないといかん。
5/6(木) 掛川・晴
日記を朝に書くのは久しぶりだなぁ。そんだけワシの知的活動レベルが下がっているって証なんだが,どーも四十路超えてから調子が良くないなぁ。厄年ってことを忘れてたけど,お祓いでもしてもらうか?
本日も昨日に続いて暑くなりそう。冬物衣類は片付けたが,羽毛布団はまだ手放せずにいた。しかしボチボチしまう時期だな。一度,クリーニングに出したいと思っているが,どこに出せばいいのやら。まぁ,しばらく悩むことにしよう。金もないし。
書き忘れていたので,今更ながら,4月のアクセス集中状況をご報告。月間単位でもそのすごさが分かる。
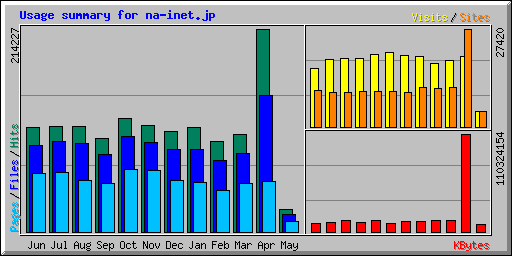
それも4月の3日間,4/24~26だけ,アクセスが集中したのだ。
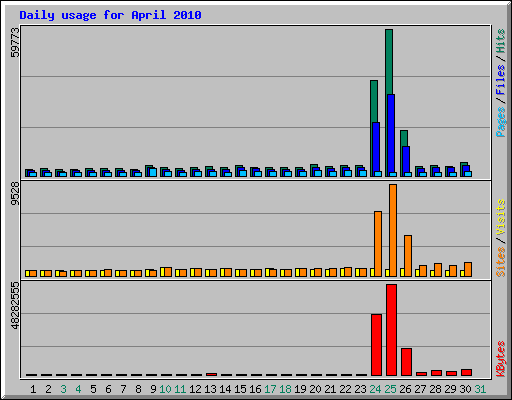
普段は3000~4000ヒットなので,その10倍以上のアクセスを処理したことになる。ま,普段がスローペースだから,10倍といっても大した負荷ではないのだが。
それもこれも,ヘタリアの画像をコピペするのではなく律儀にこっち側の画像をリンクてくれたせいである。まぁ利用はご自由に・・・ってポリシーだから,他のサービスに影響がないようなら文句を言う筋合いではないけどね。しかしワシが本来チェックしたアクセスが隠れちゃって,迷惑と言えば迷惑。
では仕事に行って参ります。