We have released BNCmatmul Ver.0.21. That dose not provide comfortable compilation but faster DD, TD, QD and MPFR prec. real BLAS functions.
遅くなりましたが,とりあえずBNCmatmul Version 0.21リリースしました。コンパイルには苦労すると思いますが,動けばそこそこ早い多倍長精度BLAS(現状は実数のみ)にはなっているかと思います。
Enjoy our world with numerical computations!
「多倍長数値計算入門(仮)」執筆ノート
We have released BNCmatmul Ver.0.21. That dose not provide comfortable compilation but faster DD, TD, QD and MPFR prec. real BLAS functions.
遅くなりましたが,とりあえずBNCmatmul Version 0.21リリースしました。コンパイルには苦労すると思いますが,動けばそこそこ早い多倍長精度BLAS(現状は実数のみ)にはなっているかと思います。
師走初日である。一気に寒くなって秋をすっ飛ばして冬になった感。富士山がきれいな季節になってしまったのである。

「多倍長精度数値計算」,Amazonの順位を見る限り「LAPACK/BLAS入門」程度には売れているらしい。せいぜい初刷分のコストを吸収できる程度には在庫が捌けてほしいものである。黒字になって困ることはないからなぁ。高いけどよろしくお願い申し上げます。
そーいや,早速誤字脱字のご指摘があったので,慌てて正誤表を追加した。こーゆー時にはやっぱりGitHubにサポート情報一切合切置いておくのは良い判断である。出版社が潰れてもファイルが残るというところが良い。いずれワシのサイトの情報は全部GitHub,ResearchGate,Researchmapに集約しておくことになるので,定年カウントダウンになったらボチボチやっておくことにしよう。
「決算!忠臣蔵」を神さんと映画の日の本日見に行った。吉本興業バックアップ映画なので,そこそこ楽しめたが,クライマックスの討ち入りシーンがないというのはどーにも肩透かし感が拭えない。溝口健二の「元禄忠臣蔵」でも見るとするかな。大河ドラマでは「峠の群像」の伊丹十三,「元禄繚乱」の石坂浩二,いずれも良い殺されっぷりであった。ワシはあれが見たいのである。
Python数値計算入門,とりあえず連立一次方程式の4章分の手前まで完成。問題はこの先で,LAPACK/BLASベースのSciPyを使う以上はせいぜい密行列用(scipy.linalg)と疎行列用(scipy.sparse.linalg)の2章にまとめてしまうのがスマートだと考えている。行列の固有値はその応用編という感じ。無駄に分厚くなるよりは,線型計算はカジュアルにお気楽に使いつつ,パフォーマンスと精度には気をつけてねという記述になれば良いかと。今月中にはここを何とかして一気に後半部分の下書きは完成させたいなぁ。
ということであと一月頑張りましょうぞ。

[ Amazon ] ISBN 978-4-627-85491-8, \4200 + TAX
いやぁ長かった長かった。本来なら昨年のうちに発売されているはずのものが,「可能な限り厚く書け」という方針に変更され,巻末のGNU MP(抜粋),MPFR(完璧),__float128(完璧)のリファレンスまで付録に付くことになってしまったからさぁ大変,シコシコ作業してどーにかこーにか248ページの,ワシの単著としては最大のページ数を誇るテキストが出来上がってしまったのである。担当編集者が途中交代したりして「こりゃ出ないかな?」などと疑心暗鬼になりつつも何とか今日の晴れの日を迎えたのだからとりあえずは良しとしよう。表紙のプログラムが本文で使っているC, C++プログラムとは似ても似つかぬものになっているなどと無粋なことをいう奴は嫌いなので無視することにして,ワシはこの分厚くてド高いテキストをしみじみ眺めて悦に入っているところなのである。
そう,本書は高価である。税抜き4200円! 吉野家の牛丼並を10杯食える値段になってしまった理由はただ一つ,特殊過ぎて売れそうにないからである。・・・んなことは分かっている,だからペラい「LAPACK/BLAS入門」程度でいいんじゃないかという提案もしていたのだが,「あれじゃペラ過ぎて演習書としては物足りない」とぬかす向きがあったらしく,「どのみち売れないんだから,そんなら分厚くしてくれ」ということになった由。開き直った結果の高額書籍なのである。つーことで,長い数字並べてヘラヘラ楽しめる,そう,「π 円周率1,000,000桁表」などをお持ちの方に置かれましては是非とも座右に置かれることをお勧めしておく。何を隠そう,ワシも本書を座右にたくさん置いているのであるからして(当たり前だ),数字マニアにおかれましては,スクラッチからプログラミングする非効率さも知っておかれては如何かと思う次第なのである。
そう,今時,多倍長計算,即ち,標準的な整数型(int, long)や実数型(float, double)を越える桁数の計算を四則演算レベルから作成するなどということは止めた方がいいのである。趣味で作るならご自由であるが,それにしても,GNU MP(GMP)やMPFR, QDといった高速かつ機能豊富なオープンソース多倍長演算ライブラリがタダで自由に使えるご時世に,それらの機能を一顧だにせずに唯我独尊的なプログラミングをすることは労力の無駄,車輪の再々発明よりたちが悪い暴挙と言わざるを得ない。本書はこれらのライブラリの解説と関数一覧(QDは初めてかしらん?),CやC++のプログラミング例を豊富に取り揃えて,あまつさえ,手間のかかるベンチマークテストまでやってお示ししているのであるから,買えとは言わないけれど(買ってくれると嬉しいけれど),スクラッチから多倍長精度プログラミングをやろうという方は一通り目通ししておくべきであると断言しておく。まぁ,Webの世界には既にこれらのライブラリをベースとした,MPACKみたいな高速計算ライブラリも多数あるので,そちらを見てもらうのも良いが,高度過ぎる複雑なライブラリを見るより,単純なCやC++テンプレート例を読んだ方が取り掛かりには良いのではないか・・・どうかは皆様で判断して頂きたい。ま,当面売り切れる本ではないので,多倍長数値計算をする必要が出てきたら,ちらとでも眺めて頂ければ幸いである。
10月超えてもまだ日中の気温が30℃を超える日が続く。台風は19号が発生し,次週の三連休には九州・沖縄近海に近づいてきて,その影響が出てくるという予報。最近は週末引きこもっているので,世間的な休日が荒れようがどうしようがどうでもいいが,収穫期に入った米などの農作物に被害が出るのは困る。全世界的に温暖化がじわじわ進んで16歳の少女まで大演説を国連でブッこく時代,ワシが死ぬまでにどんだけ強力なモンスター台風が発生するのか,楽しみでもあり,怖いようでもあり。せめて自宅リビングのガラスに保護シートでも貼らなきゃなぁとツラツラ思う。
「多倍長精度数値計算」(森北出版),Amazonにページができてた。

画像の背景のプログラムが本文で説明しているものと違うなどというツッコミは聞かなかったことにする。10月発売予定と言いまくっていたのだが,消費税増税前の駆け込み需要で印刷所が混んでおり,11月22日発売に遅延してしまったのは当方の不徳の致すところではないので謝らないよ。しかし8%に据え置かれた新聞じゃないので10%の消費税丸かぶりで¥4620っつーのは高いよなぁ。まぁGNU MPの一部とQDとMPFRとfloat128リファレンス込の,部数の見込めない本なので致し方ないところです。草稿送りつけた多倍長精度関係者には問答無用でお配りしたいところではありますが,何せ部数が部数なもので(って聞いてないけどせいぜいコミケ島角サークルの新刊ぐらいと想像),届かなかったらすいません。サポートページはすでに作ってあるんだけど,発売日と同時にリンク貼って公開予定。・・・しかしシンドかったので,MPACKの解説が欲しかったとか抜かすと丑の刻参りするぞコラ。無い物ねだりするより自分で書いてみてはと言っておく。ご本人の英語解説はこっちにあるので買うとよろしい。
Pythonプログラム,ぼちぼち追加しつつあり,Autogradパッケージを使って遊んでみた。額縁ょ〜などというものの宿命で,あれこれ余計な事務作業と書類作業が無限に割り込んでくるので,Jacobi行列で遊ぶまでには至ってないけど,接線引きまくって元の関数をイメージするグラフを書くところまではたどり着いた。
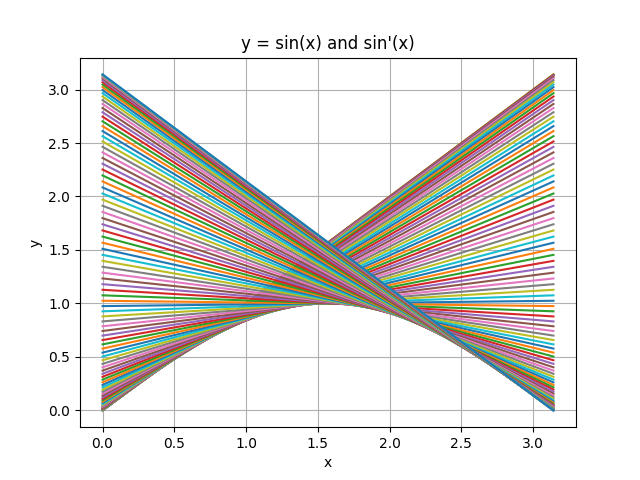
次は多段法・・・など言い出したら全然終わらないので,先に偏微分方程式の計算事例を2,3積み重ねてケリにしたい。10月いっぱいの予定,忘れてませんのでしばしお待ち下さい・・・って何度目だこの言い訳。
さて,神さんから委託されている明日の朝ごはんの準備をしよう。
台風17号が,北九州をかすめて日本海に駆け抜けていったおかげで,京都は蒸し暑い空気が淀んだ嫌な気候になったものの,風が強いが雨は降らず,昨日から開催されていたODE-JP 2019は無事閉幕したのであった。来年も無事開催できると良いが,何せ人手と場所がねぇ。

さて,明日から本格的に後期が始まる。今週の目標は
・「多倍長精度数値計算」(「入門」が外れました)の最終推敲
・再査読レポート執筆
なんだけど,当然のことながらPythonスクリプトも書かねばならぬ。今の所,
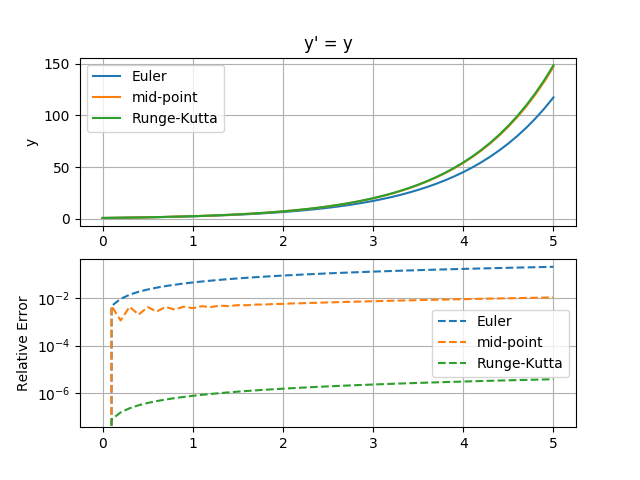
とゆーよーなグラフは書いたりしているのであります。とりあえず,次年度向けテキストはなんとかなりそうなので,どこまでPython的な課題を盛り込めるかが勝負。ま,前期にそこそこスクリプトは揃ったので,何とかなるでしょ。
ボツボツ,ブログもできる範囲でチマチマ書いていきまする。
風呂入って寝ます。