紙版 [ Amazon ] ISBN 978-4-06-522735-0, \2400 + TAX
Kindle版 [ Amazon ] \2400 + TAX

そーです,ワシが講談社刊行の自著に,「白泉社の少女漫画サイコー」と書いた大バカヤローでございます。だってホントのことだからしょうがないじゃん,少女フレンド系でハマれたマンガがなかったんだから(以下小一時間のオタク語り省略)。
それはともかく,とうとう2021年3月に出た出た出ました長年の便秘に悩んでいた末の脱糞のごとく出ましたよ旦那。前書きにも書いたが,これも偏に編集人の忍耐のシロモノなのである。こちとら,額縁ょ~の第1次任期に完全にかぶってしまい,2年目からはコロナ禍の中での対応を迫られ,おまけに科研費も当たっちまったモンだから査読付き論文の方に注力せねばならず,どーしても精神的にも時間的にも伸ばせる〆切の方を後回しにせざるを得ず,大分お待たせをさせてしまったところ,諦めもせずに待ち続けて頂いた結果,何とか「工学基礎」という極めてニッチなジャンルではあっても「ベストセラー1位」という称号を得たのだから,多少はお返しができなのかなと勝手に悦に入っているのである。まぁ出版社的には第1刷分を売り切らない限りは利益回収ができないのだから,本来は第2刷が出てから成果を誇るべきところ,どーせ初刷売り切り実績が少ないワシとしてはそんなの待っていられないので(2021年5月6日現在,Amazonのみで売り切れ状態であるとはいえ),背後に家事に勤しむ神さんの白い視線を感じつつ,まずは本書に収められなかった雑感をここに書きつけておくことにしたのである。
前書きにも書いた通り,本書は元になる原稿があるにはあった。主として静岡大学で非常勤講師を務めていた時に書き足し書き足ししながら使用していたもので,最近は本学でも使うようになったが,いかんせん近年では古い記述が増えてきたことに気づいてはいたのである。そうなると,本学でも使うようになったMATLABをベースに書き直すかなとツラツラ考えていたものの,あんな高額なライセンス料を取りくさりよってと今一つ好感を持てず,取り掛かれないまま深層学習ブームやってきてPythonが流行りになってきたところ,元原稿を基に当方を突き止めた酔狂な編集者の方が「Pythonを取るかJuliaを取るか」という二択をワシに迫ったのである。後者は権威の方が大阪大学におられるので遠慮することにし,多少は心得のあって何とかなりそう&流行には乗りたいというスケベ心が相まって,本書が出来上がったという次第なのである。
とはいえ,書き直しの必要性があることは承知していたから,章の最初に掲げた歴史的文献からの引用以外は頭から見直しをかけざるをえず,思いのほか面倒な作業であったことは前書きに書いた通りである。記憶を頼りに具体的な所を書きつけていくと,下記のようになる。
- 「第3章 Pythonことはじめ」は,もともと特定の言語を想定しての記述ではなかったので,2/3以上は書下ろし。書いてから「あ,if文の記述がなかったな」と気が付いたあたりが迂闊である。ま,プログラミング言語の素養のある人向きの書籍であるし,実装の事例は随所にあるのでそちらを見ながら補って頂きたい。
- 「第4章 丸め誤差の評価方法と多倍長精度浮動小数点計算」は,多倍長計算の章を丸ごと書き直した。下敷きにしたのはワシの紀要原稿であるが,書籍用としては記述をそのまま使うわけにもいかないず,更にリライトしてある。何せ,数多ある数値計算テキストとの差別化を図るためには丸め誤差と多倍長計算を外すわけにはいかず,とはいえワシの「多倍長精度数値計算」並みの記述を行うわけにもいかず,この長さに収めるのに苦労した。「著者の書き過ぎによる暴走」が起こらなかったのは,本章の記述を前提に紀要原稿を書いておいたおかげであろう。ワシ偉い。
- 「第6章 基本線形計算」は,計算量・ノルムの解説と,NumPyとSciPyのBLAS機能の説明をマージさせつつ,計算時間とノルム相対誤差をコードを使いながら理解できるようにした。この辺,第4章の技法を使っての検証ができるような演習問題が追加できれば申し分なかったが,サンプルプログラムを弄りながらの手すさびみたいなものになるのでキリがないのでカット。まぁ締め切り間際の強行スケジュールで無理に入れてミスを増やしかねなかったからいいか(と勝手に納得)。
- 「第8章 連立一次方程式の解法2 ―疎行列と反復法」は本来2章の分量を今の視点でまとめ直した。理論的には疎行列も密行列も違いはないが,計算量の観点からは全く違うものとして実装してあるので,まずは疎行列の解説から入り,今ではあまり見かけないSOR法系統の解説はベクトル反復が可能なJacobi反復法だけにとどめ,CG法とKrylov反復法,前処理のやり方がSciPy.sparseで簡単にできることをスクリプトとSuitSparse Matrix Collectionの実例で示すようにした。ざっくりした紹介になってしまっているのは,この辺りを詳細にやるほどの知見が著者にないせいでもあるが,この辺のまとめをちゃんとやってこなかった数値線形計算研究者らの啓蒙努力の怠慢も問題である。いくつか日本語のまとめっぽい書籍が出ていることは承知しているが「敷居が高ぇな」「門外漢には訳が分からんな」「理屈は分かったからコードにして公開してくれない?」というのが偽らざるワシの感想である。
- 「第10章 非線形方程式の解法」も2章分まとめ,ニュートン法の説明を中心に据え,代数方程式の解法はコンパニオン行列の固有値問題に帰着でき,NumPy.roots関数で簡単に解けることを示すにとどめた。減次して解くという古典的な方法も好きではあるが,まぁ現代的とはとても言えないので割愛。
- 「第12章 関数の微分と積分」と,この辺りから便利なパッケージを使うことをお勧めするように軌道変更している。微分についてはAutogradパッケージは外せないし,SciPy.integrateは次の常微分方程式との絡みが出てくるので,使い方を示すのは重要・・・と言いつつ,しっかりと等間隔分割によるニュートン・コーツ公式とガウス型公式の違いは解説しておく必要があるなと,この辺りの記述はそのまま元原稿から流用してある。二重指数積分法の説明に踏み込むと複素積分まで考えないとまずいので,今回は割愛。今の仕事が一段落したら,ロンバーグ積分と組み合わせて面白いことができないかなと夢想しているが,ここに踏み込んだら暴走が始まるので,この判断は良かった(でないと〆切が無限に伸びる)。
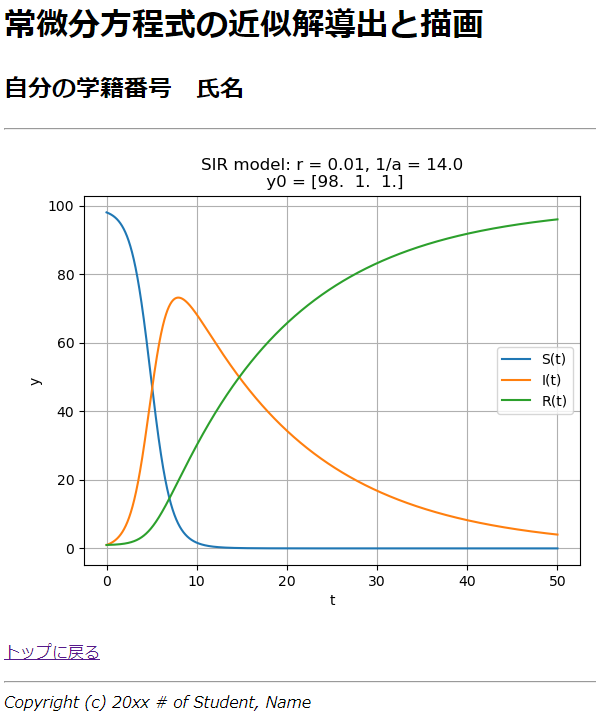
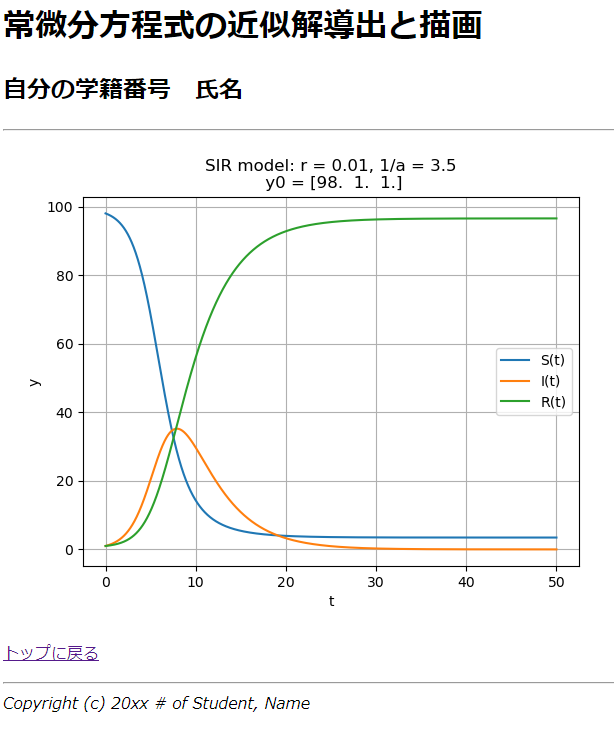
- 「第14章 偏微分方程式の数値解法」は,元原稿にない放物型・双曲型・楕円型PDE全部の実例と解説を付加した。参照した本がいずれも古くて,疎行列ライブラリが存在していない時代のシロモノで,はてさてもう少し効率的なやり方はないものかと,自分なりに咀嚼してスキームを組み立ててスクリプトを作成。疎行列以上にPDEの世界は応用分野が広いので,分野ごとに様々な独自手法が存在し,とてもじゃないが一人ではまとめきれない。ということで,せめて前章の応用としての時間発展問題ぐらいフォローしたかったが時間切れであえなくチョン。詳しい人にはPDEだけでPython本を書いてもらえばいいんじゃないかなと思うが,大規模化のためにはコアの計算部分の並列化と高速化が欠かせず,PythonじゃなくてC/C++によるMPI/OpenMPによる並列化の話になるので,もう「入門書」とは呼べないレベルになること必定である。
・・・とまぁ,このぐらいにしておくが,数値計算に限らず,プログラミングが重要な役割を果たす分野の入門書は時代の流行に合わせて言語やソフトウェアを変えながら新刊本として登場するのが常である。本書も,FORTRAN→MATLAB→BASIC→Pacal→C/C++→Pythonという流れの一つとして出たもので,類書は今後も出続けるであろうから,読者の方々は自分と相性の良いものを選んでいただきたい。本書がその一つとしてどなたかの琴線に触れることができれば,著者としては望外の幸せというものである。