数学とコンピュータに関するモロモロ – ページ 28

2014-12-102014-12-09

[没原稿] GPUを用いた高性能数値計算法の研究

　「私の研究」というテーマで学園報に原稿を依頼されたので一発目に書いたのが下記の内容。さすがに砕けすぎと読み返して判断したので硬い文章で節に分割したものを新たに書き起こして提出した。まぁ大筋最初に書いたものと大差ないんだが。つーことで没にしたのが日の目を見ないもの何なんでここに公開する次第である。

——————————–

　「コンピューターの前に張り付き，数値ばっかり打ち出しては眺めてあれこれ思案している不思議な研究」というのが，本学に着任する前に在籍していた職場の上司評であった。正確には私の出身研究室の先輩がその上司と同じところで働いており，その先輩の仕事ぶりがかくの如きの印象であったらしい。そして基本的には私の現在の研究も大差ない。ただし，目の前にあるのはGPU（Graphics Processing Unit）を積んだやたらに高熱を発するパソコンであり，眺める数値は計算結果だけではなく，数値を吐き出すプログラムの処理時間だったりする。
　現在の科学技術はコンピューター上で実行される擬似的な仮想実験，すなわちコンピューターシミュレーションが重要な地位を占めている。いっとき世間を賑わせた行政の事業仕分けにおいて「二位じゃダメなんですか？」と問われた理化学研究所に設置されているスーパーコンピューター「京」が必要とされるのも，シミュレーションの処理速度が科学技術研究の進捗の決め手になるからだ。その核心部分には微分積分の計算や，行列やベクトルの計算が繰り返し使われる。ことに後者は線型計算と呼ばれ，大規模な科学技術計算の処理速度を決める重要な核である。現在スーパーコンピューターの処理速度の全世界的な競い合いで使われるのは，巨大な鶴亀算，すなわち連立一次方程式を解くためのプログラムだが，これも線型計算の一ジャンルである。私が鈴与教育研究活動支援金を頂き，秋田県立大学のO教授・H准教授・N助教の研究グループに一か月少々混ぜて頂いて行った研究もこの線型計算の高速化へのチャレンジの一つであり，高速化のための重要なツールとしてGPUを活用したのである。ゆえに，私は２０１２年２月下旬から３月末まで，由利本荘市のキャンパスで日がな一日，パソコンの前に座ってプログラミングしては実行し，GPUによる計算の高速化の効果を調べていたという次第である。傍から見ればまさに「日がな一日パソコンに張り付いては数値ばっかり見ていた」ことになる。
　ところでGPUという名前でピンとこない方でも，近年のコンピューターゲームやCGのリアルさは良くご存知であろう。あの細かい陰影は計算処理によって生み出されており，その処理を専門に行う特殊な電子部品としてGPUは発達してきた。元々は科学技術計算とは関係のないパーツであったものが，市場原理によってドンドンその能力を高め，ついには科学技術計算の基盤である浮動小数点演算を実行できるまでに成長したのである。パソコンに詳しい方なら，AMDやNVIDIAというGPUメーカーの名前を聞いたことがあるだろう。現在隆盛なのは後者が無料の開発ツール込みで普及を後押ししているCUDA(クーダ)であり，毎年NVIDIA社が開催しているGTC Japanは数千人の来場者が訪れるイベントになっている。私の研究もこのCUDAを使って線型計算を高速化した上で，微分方程式の数値解を高速に導出するために応用することを目指して行ったものである。この研究結果の詳細は静岡理工科大学紀要第２１巻(2013年)に掲載されているのでご興味ある方はWeb上からも読めるので参照されたい。以下，その概要について簡略化して述べることにする。
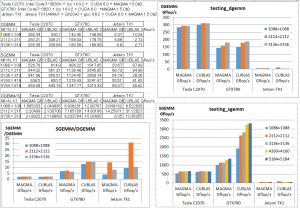
　CUDAの良いところは，市販のパソコンに搭載されるグラフィックスカード(但し，NVIDIA社のGPUが搭載されているものに限る)を買ってきてデスクトップパソコンの拡張スロットに刺せばすぐに開発に着手できることにある。とは言え，そこは商売，NVIDIA社のGPUであれば何でも良いというわけにはいかない。特に科学技術計算では桁数の多い浮動小数点演算が不可欠であるが，市販の安いグラフィックスカードでは単精度(１０進約７桁)の浮動小数点演算を高速化するのがせいぜいで，主流の倍精度（１０進約１６桁）の計算を行うにはより高価な科学技術計算専用のGPUが必要となる。そこで理工科大学の学内研究費の援助を得てTesla(テスラ)C2070という高価なGPUを搭載したコンピューターを購入し，CUDAプログラムの開発にはもっぱらこのマシンを利用して倍精度線型計算の高速化を追求した。結果としては既存のものより２倍以上の高速化が達成でき，これを土台として構築した常微分方程式の数値解計算も，大規模問題になれば最大数十倍まで高速化できることも分かった。
　GPUは組み込み用の小型コンピューターやスマートフォンでも普通に搭載されている。この研究の延長として，今年度はJetson TK1という小型の組み込み用コンピューターボードを購入し，線型計算のベンチマークテストを行ってみた。今のところ，大規模計算には向いていないが，数年前のパソコン以上の能力は持っており，今後急速に能力アップするに違いない。スーパーコンピューターから組み込みコンピューターまで幅広く使用できるGPUの能力を最大限生かすべく，本研究を継続していきたいと考えている。

2014-10-122014-10-12

“Fast matrix multiplication is stable,” but…

　今年(2014年)の3月に応用数理学会連合研究会で多倍長Strassenアルゴリズムについて喋った時に，”Group-theoreticアルゴリズム”の話がちょろっと出たので，Strassenの件が落ち着いた時にちょっと調べてみたのである。・・・なるほど確かに「一時は」盛り上がっていたようだが，実装に絡む大事な論文が消えてしまって以来，どーも最近雲行きが怪しいようなのである。とはいえ，面白そうな話題ではあるし，ちょっとずつ勉強していくには良さそうなものなので，コメントいただいた方に対して「一応は調べてみましたよ」という報告がてら，この記事を起こしたという次第である。「実装に絡む大事な論文」のその後や”Group-Theoreticアルゴリズム”の動向をご存知の方がいらっしゃったら情報も頂けると幸いである。

　つーことで多倍長Strassenの論文掲載が決まったので，ソースも外に出した。ろくすっぽ整理してない代物なのだが，ちょろっと引き合いもあったこともあって，ちゃんと動いているという証拠物件なので早めに出すことにしたのである。
　ちなみにこれ，比較対象のため倍精度の行列積もIntel Math Kernel(IMKL)提供dgemm関数を利用して実装しており，その結果については紀要原稿に書いてある。ま，メインは多倍長行列積の方なので，あくまで比較用なのだが，存外実装が難しいなぁという感想を持った。特に2^nでない行数・列数の時の処理が大変で，今のところは多倍長に合わせてパディング（0要素を詰め込んで2^nの倍数の行数・列数にする)とピーリング(2^nの倍数をはみ出る部分はブロック化して別に処理する）処理を組み合わせて実装しているが，ATLASベースのStrassen実装報告にある通り，倍精度ぐらいだとパディングだけでサイズ合わせをした方が無難かもしれない。ちなみに奥村先生の「C言語によるアルゴリズム事典」「Javaによるアルゴリズム事典」にもStrassenのアルゴリズムの話題があるが，1988年のBailey論文での成果を元にしている「2048×2048の行列積で5割高速」という記述をそのまま真に受けるとバカを見る，ということはATLASベースの実装とワシのやったIMKLベースの実装，両方の結果を見てもらえばご理解いただけるだろう。現在までのStrassenアルゴリズムのサーベイについてはワシの紀要原稿にもちらと書いたが，スポック博士の分厚い本の23章が一番コンパクトにまとまっているので参照されたい。

　つまり倍精度計算だと，キャッシュヒット率・SIMD命令の活用・メモリ操作関数のパフォーマンスによる影響が大きく処理時間に作用することになるので，演算量を多少減らしたところで，Strassenアルゴリズムを実行するために必要となる前処理・後処理をも含めると，全体として処理時間が減らせるかどうかはやってみないとよく分からないところが大きいのである。その点，元々四則演算の処理速度がトロい多倍長計算だと，演算量の減少がダイレクトに処理時間の減少に繋がるので大変分かりやすい結果になる。つーことで任意サイズの行列積の計算がStrassenアルゴリズムで可能になれば，LU分解の処理時間も最大3割減となるのである。逆に言えば，今時倍精度計算でLU分解に適用しても，PC単体のオンメモリで収まるサイズの問題程度では殆ど効果はないのでは，と思えるのである。Bailey先生のCray-2と今のx86環境とでは，キャッシュやSIMD命令をサポートしたアーキテクチャも大分異なっているので，同一視してはいかんのである。

　そんだけ，今の計算環境では高速だが前処理・後処理の複雑なアルゴリズムの実装は職人芸が必要であり，ましてやStrassenやWinogradアルゴリズムよりも複雑怪奇な”Group-Theoretic アルゴリズム”って奴の実装は相当な困難が予想される。これについてはオリジナルがこれで，それに対して誤差解析の観点から”Stable”という判定を下した（イマイチ疑問があるのだが）論文がこれであるらしい。後者については査読論文になっているようなので（これ），内容的にどうこういう気はないのだが，問題は後者の奴にある参考文献[8]。どうやら実装した結果についての報告らしいのだが，検索しても見つからないし，同様に実装した結果について記述したものが一つも見つからないのである。どなたかチャレンジして失敗したって記述でもあるなら分かるんだが，どーも今のところちゃんと実装した人が一人もいないんじゃないのかとワシは大いに疑っているのである。参考文献[8]が見つからないのは実装に失敗したか，作ってみたけど倍精度程度では高速にできなかったんじゃないのかな～，と今のところ考えている。ま，Strassenアルゴリズムの結果を見る限り無理もないかなぁとは思うのである。前処理と後処理にめんどくさそうなFFT?を使っていようだから，かなり難しいんじゃないのかしらん？　まぁだからこそ「多倍長でやってみたらいいのでは」というご意見も分かるんだけど，さーて・・・？

　と，この先はワシが考えていけば済むことなので，少し時間をかけてアルゴリズムを解読してみるが，何分，かなり浮世離れした感のある研究テーマだし，その後の進展が聞かれないところを見ると，いろいろ実装上の困難もありそうである。だからこそのチャレンジングなテーマとも言えるけど，そういうのはもっと頭のいい人に取り組んでもらえないかなぁと思っているのである。もしどなたか既に着手されてそれなりの成果が出ているようでしたら，お知らせ頂ければ幸いなのである。あ，黙っていてくれと言われれば黙ってますのでこっそりでも結構でございます，はい。

2014-09-112014-09-11

「まえがき」候補（１）

現代の様々な高性能コンピューター上で高速な密行列・ベクトル計算が実行できる，そういうソフトウェアが実現できないものだろうか？　できるとすれば，どうやればいいのか？　その疑問に答える，つまり，実際にその理想を実現するソフトウェアを提供すること，それがLAPACKプロジェクトの目的なのである。(P.54, LAPACK User’s Guide Ver.3.0)

　本書はLAPACK(Linear Algebra PACKage)とそれを下支えするBLAS(Basic Linear Algebra Subprograms)，そしてそれらから派生して登場した疎行列ライブラリであるSparseBLAS，GPU用のcuBLAS, cuSPARSE，そしてMAGMA(Matrix Algebra on Gpu and Multicore Architectures)の基本的な使い方をざっくりと解説した概説本です。各ライブラリの詳細についてはリンク先にある文書群をご覧頂きたい，という開き直った態度で執筆されており，「そういうWeb上の情報があれば事足りる」というエキスパートな方々には無用の長物であります。なんでも検索すれば見つかるというわけじゃありませんが，こと本書にのべられている事項は大体見つかるものばかりです。LAPACKやMAGMAについて，まず手っ取り早く知りたければ下記の二つの文書を読むことをお勧めします。

細田陽介「私の研究開発ツール第70回　数値計算パッケージの使い方」
http://www.ite.or.jp/data/journal/passed_issues/tool1309/
中田真秀 BLAS, LAPACKチュートリアル
- (1) http://www.jsces.org/Issue/Journal/pdf/nakata-0411.pdf
- (2) GPU編 http://www.jsces.org/Issue/Journal/pdf/nakata-0711.pdf

　読んだ上で「あ，大体わかった」という人はお呼びではありません。「よく分からないなぁ」と感じた方，それが本書が対象とする読者です。そして著者である私も，これらの文書類を読み，プログラムを片手間に弄っても「よく分からない・・・」と感じておりました。これらの文書類が悪いのではなく，原因は後述するように，それ以外のところにある訳で，それ故に本書を執筆することになったのです。本書は私のそうした知的（？）欲求不満から生まれたものなのです。

　私の抱いた欲求不満を分析してみると，次の点にあるようでした。

LAPACK/BLAS（とその派生ライブラリ)の歴史的背景が分からない
LAPACK/BLASの提供する関数の名付け方(naming scheme)が古いFortran由来で分かりづらい
そもそもFortranベースのライブラリをC/C++から使おうとすると細かい齟齬が生じてイライラする
何でそんなにみんなLAPACK/BLASを使うのかよく分からない→自分の仕事にどう役立つのか分からない
大学カリキュラムの「線型代数」の知識とLAPACK/BLASが提供する機能の関連が分からない

　歴史的背景については，端的にまとまった（私レベルが理解できる）文献がないという事情がありました。LAPACK/BLASが生まれてきた時代的・コンピューター的な歴史を俯瞰したかったという欲求がここで生まれ，簡単な年表を作り，それに基づいて私が理解できた範囲の解説を付記しました。人間，中年を超えると歴史に興味が自然と湧くといいますが，実際，年表づくりは楽しい作業でした。

　LAPACK/BLASの関数名のつけ方は，もともと古い時代のFortranにあった，関数とサブルーチン名の8文字制限というものに起因しています。現在でもLAPACK本体はFortran77ベースの記述がされており，C/C++や種々のオブジェクト指向言語に慣れ親しんだ世代には呪文のようなものに見えてきます。もちろんマニュアルにはちゃんと名付け方の解説はあるのですが，「関数名」と「（特に行列の）データ構造」をリンクして覚えておかないと，使いたい関数を索引から調べても，「えーっと行列はどういう風に格納するんだっけ？」となってしまいます。今でもFortranを愛用する方にとっては便利でも，C/C++的言語で書きたい多数派にとっては取っつきづらい「歴史的背景」を持ったLAPACK/BLAS。それを「最初からC/C++でプログラミングする！」と宣言した解説書を私は念願しておりました。

　加えて，行列のデータ構造も分かりづらさの原因の一つです。それは行列のデータ構造が，線型代数で習った「対称行列」・「エルミート行列」・「直交行列」・「ユニタリ行列」・・・といった数学的性質に基づくものに由来して決まるものもあれば，「密行列」vs. 「疎行列」（「帯行列」・「三重対角行列」等）というメモリ・計算効率的な理由によって決まるものが混在していることにあります。この両者をきちんと整理して把握する解説文書を私は強く欲しておりました。

　そして，LAPACK/BLASが持て囃される理由も，ちゃんと自分の手でプログラミングした応用ソフトウェアを実装したうえで理解したい訳です。もちろん人によって興味の対象は千差万別ですが，本書では，上記の解説を行うことで，各人の興味の対象物へのアプローチを用意できたのではないでしょうか。

　Python/PHP/Rubyといった使いやすいライブラリを備えたコンピュータ言語，Matlab/Scilab/Octaveといった統合型数値計算ソフトウェア，Mathematica/Maple/Maximaといった記号処理を得意とする数式処理ソフトウェアが誰でも手に入れられる時代に，ハードウェアに密着したコンパイラ言語からしこしこプログラムするというニーズは現代では量的には減っていると感じます。しかし，一部の高速性を追求するマニアや組み込み機器開発用，そしてマシンごとのアーキテクチャに最適化して大規模計算を行うニーズは確実に残っています。本書ではその一端をざっくりと解説しただけの荒っぽい本ですが，私が抱いた欲求不満を共有する方々の知識導入時にはこそこ役に立つものになっているハズ。そして皆様の知的好奇心を満足させた暁には，本書の様々な欠点や間違いを指摘できるようになっているハズであります。もし本書についての苦情やお問い合わせをしたければ，サポートページを通じて私にお知らせ頂くか，SNS,Web上でその勉強の成果を開陳して頂きたいと念願しております。最終的には，その成果をソフトウェアや文書等，「形」なったものを通じて世に発信して頂ければ，望外の幸せであります。

2014年9月11日(木)
遠州茶畑のど真ん中にて
静岡理工科大学　幸谷智紀

2014-08-12